Les calculateurs auraient certainement pu progresser encore longtemps sans devenir des ordinateurs. Entre les deux, il n'est pas qu'une simple différence de degré. Nous verrons que l'ordinateur introduit plusieurs différences majeures par rapport aux calculateurs. Pour le comprendre, nous devons revenir en arrière dans le temps. L'histoire de l'ordinateur proprement dit commence bien avant ses mises en œuvre matérielles, avec des recherches fondamentales de logique et d'algorithmique qui mettent en jeu des objets mathématiques très abstraits. Leur réalisation attendra la “faveur” de la seconde Guerre mondiale et de la guerre froide qui s'ensuivra. Plus encore, l'informatique s'appuie sur de nombreuses évolutions (voire révolutions) conceptuelles très antérieures, de l'ordre du siècle parfois. Toutes sont liées à la communication en général ou aux télécommunications en particulier.

L'élément le plus central de toute théorie de l'information, le changement conceptuel le plus fondamental, est la séparation fond-forme, l'articulation arbitraire qui peut s'établir entre un signifié et un signifiant, pour formuler cela en termes modernes (Ferdinand de Saussure, 1857-1913). Cette séparation, fondamentalement en germe dans le principe de l'écriture alphabétique, avait déjà intéressé les théoriciens du langage antiques et médiévaux, avant la linguistique moderne. Elle existait également dans un autre champ très pratique, là aussi depuis l'Antiquité, celui du cryptage de la correspondance pour des raisons de confidentialité, quel que soit son transport : à pied, à cheval ou électrique. Une des méthodes, simple, consistait à remplacer des lettres, des mots ou des expressions par des écritures spécifiques connues des seuls émetteurs et destinataires.

Issue de ces réflexions sur le langage et de la nouvelle algèbre, qui se met en place au 19^e siècle, la logique moderne reprend systématiquement et à nouveaux frais la question de l'articulation entre le sens, en particulier les valeurs de vérité (vrai/faux), et les notations, particulièrement dans le domaine mathématique. Dans un premier temps, suivant des principes remontant à l'arithmétique binaire de Leibniz (17^e s.: 1646-1716) et au diagrammes d'Euler (18^e s.: 1707-1783), les travaux de George Boole (19^e s.: 1815-1864) définissent une algèbre, un calcul, des valeurs de vérité. Ces travaux eurent un impact considérable sur la logique naissante du début du 20^e siècle. On montra, dès la fin du 19^e siècle, que cette logique pouvait être mise en œuvre par des relais “téléphoniques”^[6].

Parmi toutes les questions théoriques qui intéressaient la logique à cette époque, une en particulier fut déterminante pour l'informatique. Beaucoup de mathématiciens pensaient à l'époque que le travail de démonstration mathématique était “mécanique” et qu'il était en principe possible de concevoir un procédé systématique permettant (potentiellement au bout d'un temps très long) de résoudre toute question bien formulée. Cette idée conduisit dans un premier temps à axiomatiser les mathématiques, puis, dans un second temps à formaliser la notion-même de procédé de calcul.

Aujourd'hui on appelle « algorithme » un procédé de calcul décrit de façon systématique. Il permet, certaines données étant fournies, de produire un certain résultat (généralement la solution d'un problème donné). On connaît depuis l'Antiquité (au moins) de tels procédés, par exemple l'algorithme d'Euclide qui permet de poser une division de nombres entiers. Le nom « algorithme » a été donné en l'honneur du mathématicien perse Al-Khwârizmî (~780-~850) qui est à l'origine de la notation symbolique et de l'introduction du zéro indien dans l'aire culturelle arabe et qui rédigea une encyclopédie des procédés de calcul connus à son époque. Dans le domaine de l'automatique, le mot sera conceptuellement renforcé au 19^e siècle par Ada Lovelace (1815-1852). Les logiciens du début du 20^e siècle, en particulier Kurt Gödel (1906-1978), Alan Turing (1912-1954) et Alonzo Church (1903-1995), firent de ces algorithmes des objets mathématiques, à propos desquels il devenait donc possible de démontrer des théorèmes.

Jusqu'aux années 1930, les mathématiciens pensaient généralement qu'il existait des algorithmes pour résoudre chaque problème et même un algorithme universel susceptible de trancher tout problème. Émise par Leibniz, cette hypothèse sera formulée en termes rigoureux par le mathématicien David Hilbert (1862-1943) : existe-t-il un procédé mécanique permettant de trancher tout problème mathématique formulé de manière précise ? Hilbert était un immense mathématicien, très influent, et ce programme suscita de nombreuses recherches, dont émergea la logique mathématique. Les travaux de Gödel, Turing et Church montrèrent par trois approches différentes qu'un tel procédé ne peut pas exister.

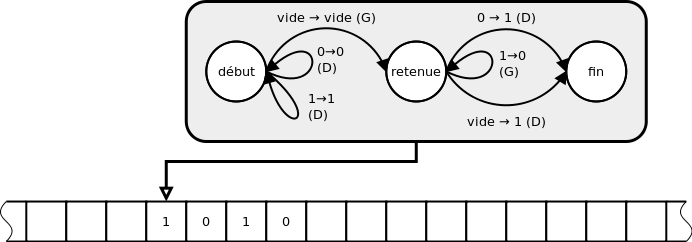
L'objet mathématique inventé à cette fin par Turing, qu'il décrit en 1936, donc bien avant les premiers ordinateurs, est sa fameuse « machine de Turing »^[7]. Ses principaux éléments sont : une bande infinie constituée de cases mémoire, un module de lecture/écriture de la bande et une unité de contrôle automatique permettant à chaque étape d'écrite une donnée puis de se déplacer à gauche ou à droite, le tout en fonction de son état antérieur. Il s'agit bien d'un dispositif universel : il permet de mettre en œuvre n'importe quel algorithme. Précisément (c'est ce qu'on appelle la « thèse de Church ») : tout traitement d'information réalisable mécaniquement peut être mis en œuvre par une machine de Turing appropriée. Si la machine de Turing avait eu une contrepartie matérielle, ç'aurait été la première machine à programme enregistré capable de traiter de façon universelle de l'information, autrement dit le premier ordinateur. La thèse de Church peut s'interpréter, aujourd'hui, en disant que tout traitement systématique d'information peut être réalisé par un ordinateur correctement programmé et suffisamment puissant. Attention : ceci ne signifie pas que tout problème est résoluble mécaniquement, seulement que ce qui est résoluble mécaniquement l'est informatiquement.

Figure 1.4. Une machine de Turing ajoutant un à un nombre écrit en numération binaire

Dans son article de 1936, On Computable Numbers with an Application to the Entscheidungsproblem, Turing fonde ainsi l'informatique, à la fois la science informatique et ce qui sera plus tard la technique informatique. Il donne aussi la première définition systématique des programmes informatiques.

Conceptuellement, ce précurseur théorique des ordinateurs est fondamentalement immatériel puisque les machines de Turing ne sont rien moins que des objets mathématiques. Un autre fait aura une incidence historique considérable : la notion-même de machine universelle porte en elle le fait que programmes et données, tous les programmes et toutes les données, sont fondamentalement de même nature.